Unofficial Stationeers Wiki Unofficial Stationeers Wiki

Pressure, Volume, Quantity, and Temperature

In this article, I will take you through the physics relating Pressure, Volume, Quantity and Temperate. I will then take you through a few example of applying it using the same style that you find in a high school text book. FUN!

Side note: I use engineering notation here sometimes. For example, one thousand can be shown as 1E3. I may also use a 'k' too, but that can sometimes be confused with the K for Kelvins, so I try to stay clear of it.

Side side note: These calculations are greatly simplified and account for one variable change at a time.

Definitions

Pressure: This is the physical force applied on the walls of the containing vessel. Measured in Pascals. Also known as Pounds Per Square Inch (PSI) in antiquated system.

Volume: This is a measure of the physical space that the gas occupies. Measured in Liters. 1 Liter is equal to the space contained in a 10 x 10 x 10 cm space. (Or Approximately 3.94 x 3.94 x 3.94 Inches in ancient times).

Quantity: The number of particles contained in a particular space. In our case, it is the number of molecules measured in moles. 1 Mole = 6.022E23 molecules. (or around 602,200,000,000,000,000,000,000 molecules. ).

Temperature: A measure of the thermal energy of the gas. Once measured in Fahrenheit (in the dark times), now measured in degrees Celsius or Kelvin. To convert from Celsius to Kelvin, simply add 273.15. It is impossible to have a negative value on the Kelvin scale.

Relating them all together

All four of the above values balance each other in any given system. A change in one will effect the others. But that applies only in real world. In this game there are some limits:

• Only things that have atmosphere have temperature.
• Anything facing vacuum will lose heat unless it is insulated.
• Anything facing sunlight will gain heat.
• All finished walls and finished cube frames are perfect insulators. Windows allow radiation from sun.
• Like real world, increasing temperature will increase pressure. Lowering temperature will lower pressure.
• Unlike real world, raising pressure will not raise temperature. Lowering pressure will not lower temperature. This prevents making own heat transfer designs using only pressure.

For example

Let's pretend that we have a 100 liter container of some gas. We squeeze that container down to 50 liters. What would happen to the quantity, pressure, and temperature?

Well, the quantity would stay the same, obviously. Pressure will most likely increase. But what about temperature? Well, as it turns out, it will increase as well (but not by a lot... Most of the change is in pressure).

So how exactly do all these values play with each other? The answer to this question lies in the ideal gas equation:

P * V = n * R * T

Where:

• P - Pressure in Pascals
• V - Volume in Liters
• n - Quantity in moles
• T - Temperature in Kelvin
• R - Ideal Gas Constant (in this case, we use 8314.46261815324) in unites of (deep breath..) Liter Pascals per Kelvin moles (Lit * Pa)/(mol * deg K)

So, if we had a furnace with 2 mol of gas in it at 300 degrees Kelvin, what would be the pressure? (A furnace has a 1,000 liter capacity)

Rearrange for Pressure:

P = (nRT)/V
P = (2 * 8314.46 * 300)/1000 = (approx) 5 kPa (or 5000 Pascals)

Similarly, you can rearrange this equation to solve for volume, temperature, and quantity as needed.

Volume Pump Example

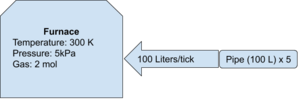
Using the same conditions as above, assume there is a volume pump attached to the input (like you find on an advanced furnace. If you're poor and can't afford an advanced furnace, use a regular furnace with an attached volume pump on the inlet. You hobo). Assume the pressure behind the volume pump is at a steady 50 Megapascals (50E6 Pascals) at 200 Kelvin and there is 5 pipe segments (100 Liters per pipe segment = 500 Liters). The stationer (being dumb, I guess) turns the pump up to 100 Liters. How much pressure is going to be added to the system on each game tick? Should the stationeer be sh***ing their space suit?

Now is a good time to mention that the dial on a volume pump is actually a measure of rate, not volume. When setting the volume pump to 10 Liters, it actually means "10 Liters per game tick". WHY it's just labelled as volume and what determines a game tick? I don't know, go ask the devloper - I'm busy.

First thing you need to figure out is now many moles of gas is in the pipe per liter. So, rearrange the magical equation for n:

• n = (PV)/(RT)
• R = 8314.46 (This is always the same.. That's why they call it a 'constant)
• T = 200 Kelvin
• P = 50E6 Pascals
• V = 500 Liters of pipe (5 segments, each holding 100 Liters)

You can also calculate the number of moles in the pipe and divide that by the volume of the pipe (each pipe segment is 100 Liters):

n = (PV)/(RT) = (5E6 * 500)/(8314.46 * 200) = 1503.4 moles of gas in the pipe.

1503.4 moles of gas contained in 500 Liters of pipe means each liter has 1503.4/500 = approximately 3 moles of gas per Liter.

So, each game tick 100 Liters of gas is pumped into the furnace. Each liter contains 3 moles of gas, which means that each game tick 300 moles of gas is pumped into the furnace.

How much pressure does 300 moles exert in the furnace? Arrange the equation to solve for pressure:

P = (nRT)/V

Where:

• n = 300 moles
• R = 8314.46 blah blah constant blah blah
• T = 300 degrees kelvin (remember, the furnace was a bit warmer than the pipes..)
• V = 1000 Liters (the volume of the furnace). "Go throw a log in the ten piper", grandpa would say..

P = (nRT)/V = (300*8314.46*300)/1000 = 748301 Pascals (or 748 kPa).

So, each game tick will add 748 kPa to the furnace at this rate. That's pretty quick. Not space suit soiling quick, but it can get out of hand if you're not careful. The furnace will blow around 60 MPa (I think) so....

Extra Credit!!

For those of you that are really keen, you can use calculus to compute rates. Assuming everything else remains constant, just differentiate the equation according the variables you need. So, if you want to know what the rate of change for pressure with respect to quantity (moles) you can:

P = (nRT)/V
dP/dn = (d/dn)(nRT)/V = (RT/V)*(dn/d)n = RT/V (in unites of Pascals per mole)

Change in temperature with respect to the change in pressure: T = (PV)/(nR)
dT/dP = (d/dP){(PV)/(nR)} = {V/(nR)} * (d/dP)P = V/(nR)